Perplexying Python
This challenge is from MetaCTF 2022, the challenge literally had zero solves till the CTF ended, so i decided to go back to the challenge, a zip file was given:

unziping the zip file we saw two python files:

content of main.py :
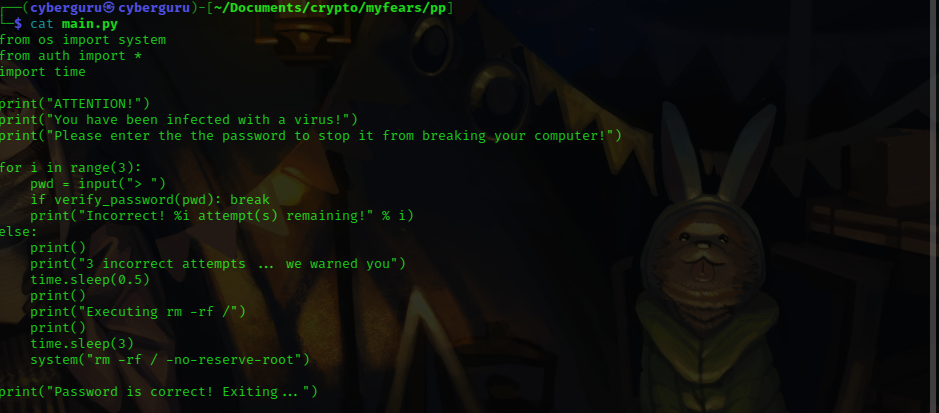
from the content of the main.py we could see that the program ask us for a password and verify it by passing it to verify_password function
if the password is wrong it print’s some dangerous statement that everyone fears 😆
running the main.py file we have:
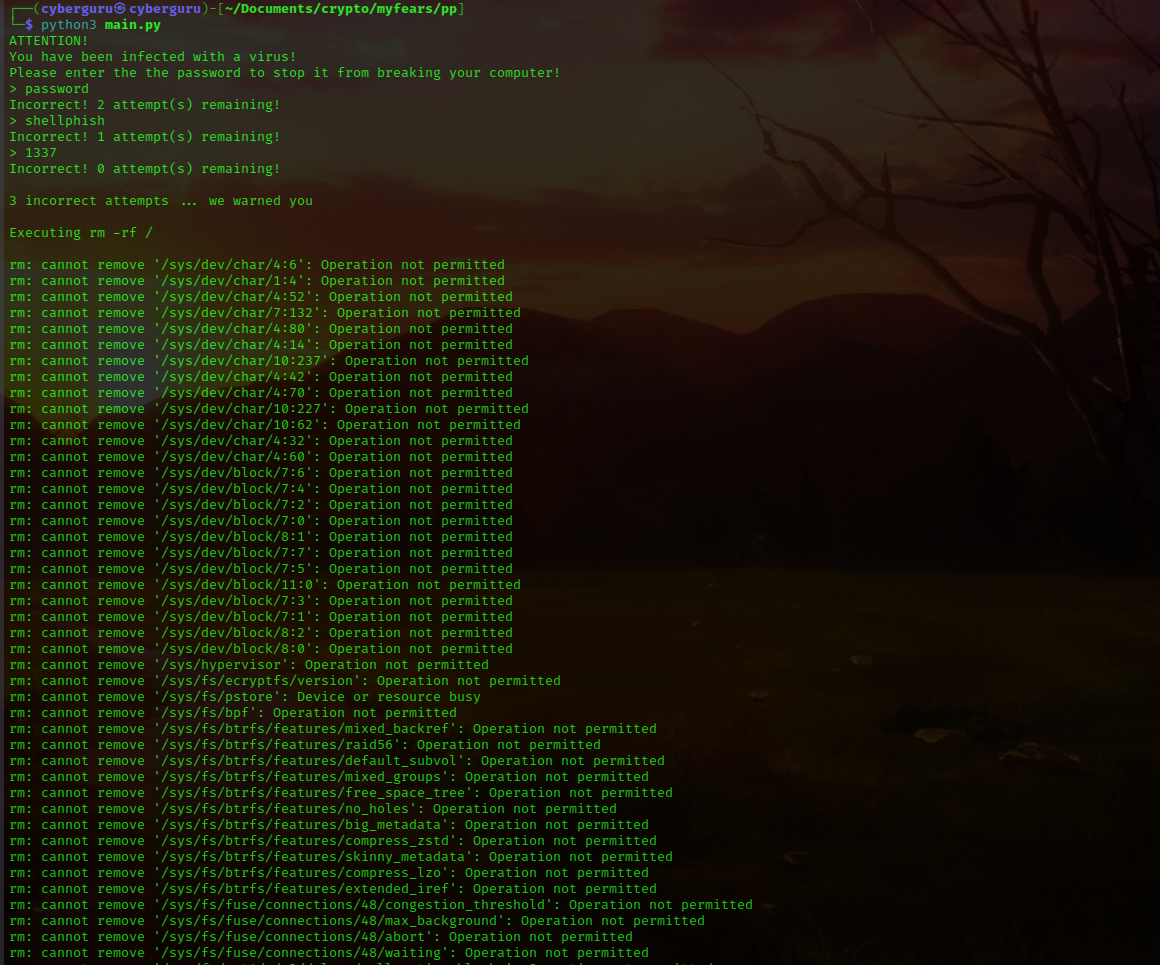
we could see the impact of inputing wrong password with only 3 attempts….
content of auth.py :
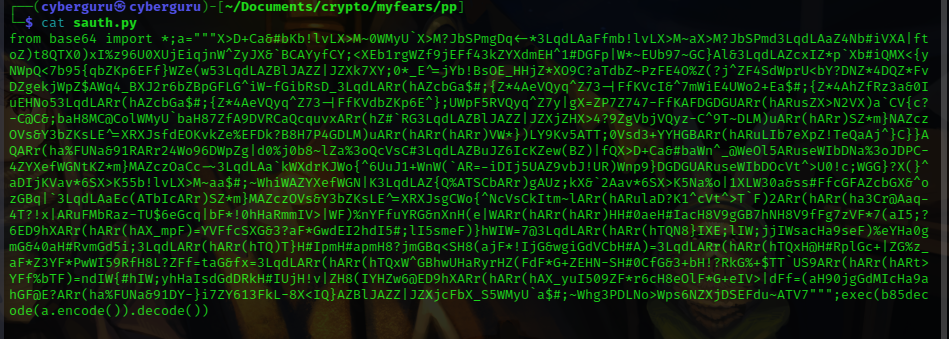
we could see the content of auth.py has some base encoded text, de-encoding it we have:
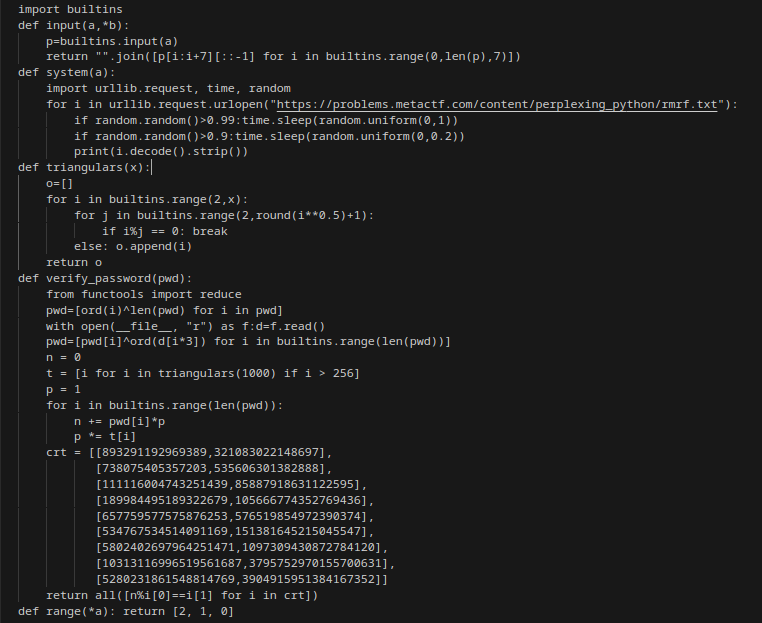
let’s break down the functions:
def input(a,*b):
p=builtins.input(a)
return "".join([p[i:i+7][::-1] for i in builtins.range(0,len(p),7)])
The first function takes care of our input, the function collects our input and randomize it by taking 7 characters at a time and reversing it then returns the combined combination
def system(a):
import urllib.request, time, random
for i in urllib.request.urlopen("https://problems.metactf.com/content/perplexing_python/rmrf.txt"):
if random.random()>0.99:time.sleep(random.uniform(0,1))
if random.random()>0.9:time.sleep(random.uniform(0,0.2))
print(i.decode().strip())
The next function emulates the system function to print out random text gotten from the remote url.
def triangulars(x):
o=[]
for i in builtins.range(2,x):
for j in builtins.range(2,round(i**0.5)+1):
if i%j == 0: break
else: o.append(i)
return o
The triangulars function returns a range of number from 2 to i^(0.5)+1
def verify_password(pwd):
from functools import reduce
pwd=[ord(i)^len(pwd) for i in pwd]
with open(__file__, "r") as f:d=f.read()
pwd=[pwd[i]^ord(d[i*3]) for i in builtins.range(len(pwd))]
n = 0
t = [i for i in triangulars(1000) if i > 256]
p = 1
for i in builtins.range(len(pwd)):
n += pwd[i]*p
p *= t[i]
crt = [[893291192969389,321083022148697],
[738075405357203,535606301382888],
[111116004743251439,85887918631122595],
[189984495189322679,105666774352769436],
[657759577575876253,576519854972390374],
[534767534514091169,151381645215045547],
[5802402697964251471,1097309430872784120],
[10313116996519561687,3795752970155700631],
[5280231861548814769,3904915951384167352]]
return all([n%i[0]==i[1] for i in crt])
The verify_password function takes in the password, the function now xor’s the pwd with the length of the pwd, it then open the whole file (the auth.py file) and xor the pwd with iteration of every i*3 character in the file
The function further computes t by list comprehension of numbers in triangulars(1000) that are greater than 256, it now loop through in the range of length of the list pwd and sum up the product of each content of t[i] multiplied with pwd[i] storing it in n and also stores the product of p
At the end of the function we saw an array of list containing large numbers then a return statement that returns the modulo operation n % i[0] == i[1] for every element in the crt list, False if every element in the list is False or contains a False and True if every element in the list is True.
def range(*a): return [2, 1, 0]
The last function emulates the range function in python but returns only [2, 1, 0
Breaking The Challenge
From the Last operation in the verify_password function we could use the crt list to compute the value of n , from the Concept of Chinese Remainder Theorem which state a number can be represented in linear congurence by it’s remainder and modulos, using the CRT algorithm we got n as :

using n we could recover pwd with the help of t we could compute t from
t = [i for i in triangulars(1000) if i > 256]
then we now compute a mapping using the product of each index from base of t :
tt = [257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
mappings = []
t = 1
for i in range(len(tt)):
mappings.append(t)
t *= tt[i]
Since the operation n // t == p[i] holds true, we could recover pwd :
pwd = []
for i in mappings[:-65][::-1]:
res = xx // i
xx -= res * i
pwd.append(res)
pwd = pwd[::-1]
we got a relative small number at index 65 of the mapping, so this is possibly the length of the pwd, we went further and compute the result and store it in pwd, we then reverse the pwdsince our operation started by recovering the last character of thepwd list.
Next phase is to xor the content of pwd with the file:
with open("sauth.py", 'r') as f:
d = f.read()
pwd=[pwd[i]^ord(d[i*3]) for i in range(len(pwd))]
Next we xor the current content of pwd with the length 65:
pwd=[i^len(pwd) for i in pwd]
At this point we were able to compute the content of the pwd list as seen from the verify_password function, we now go pack to the input function were our pwd was reversed 7 by 7 length and appended, we simply reverse this function by computing it with:
g = [pwd[i:i+7][::-1] for i in range(0,len(pwd),7)]
Then we combine the result and convert it to Characters:
flag = []
for res in g:
flag = flag + res
print(''.join([chr(x) for x in flag]))
Combining all this, Behold, our final script:
#!/usr/bin/python3
#xx gotten from chinese remainder theorem
xx = 1007530794370674919528700858409178961234447429005443823520140030680322196270661110990236896504373773579753972016930268730878278
tt = [257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
mappings = []
t = 1
for i in range(len(tt)):
mappings.append(t)
t *= tt[i]
with open("sauth.py", 'r') as f:
d = f.read()
pwd = []
for i in mappings[:-65][::-1]:
res = xx // i
xx -= res * i
pwd.append(res)
pwd = pwd[::-1]
pwd=[pwd[i]^ord(d[i*3]) for i in range(len(pwd))]
pwd=[i^len(pwd) for i in pwd]
flag = []
g = [pwd[i:i+7][::-1] for i in range(0,len(pwd),7)]
for res in g:
flag = flag + res
print(''.join([chr(x) for x in flag]))
Running the script we have our pwd/flag :

this_virus_works_in_every_os_except_suicide_linux
Remarks
well looking back i couldn’t have solved this Challenge back then during the CTF with the amount of knowledge/experience i had then 😕 , but with constant grinding and learnning i was able to come back and solve it. It was a nice challenge that required critical thinking which i love the most 😄